问题
解答题
已知圆的内接四边形ABCD的边长分别为AB＝2，BC＝6， CD＝DA＝4，
（1）求角A的大小；
（2）求四边形ABCD的面积．
答案
（1）A＝120º（2）8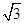
题目分析：（1）解三角形问题，一般利用正余弦定理进行边角转化. 由面积公式有四边形ABCD的面积S＝S△ABD＋S△BCD＝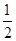
AB·AD·sinA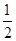＋BC·CD·sinC，∵A＋C＝180º∴sinA＝sinC∴S＝16sinA．由余弦定理得：BD2＝AB2＋AD2－2AB·AD·cosA＝20－16cosA，BD2＝CB2＋CD2－2CB·CD·cosC＝52－48cosC，∴20－16cosA＝52－48cosC解之：cosA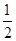＝－ , 又0º＜A＜180º, ∴A＝120º，（2）由(1)有四边形ABCD的面积S＝16
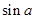，所以S＝16sin120º＝8.
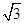解：四边形ABCD的面积S＝S△ABD＋S△BCD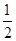＝AB·AD·sinA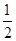＋BC·CD·sinC
∵A＋C＝180º∴sinA＝sinC∴S＝16sinA．
由余弦定理得：BD2＝AB2＋AD2－2AB·AD·cosA＝20－16cosA，
BD2＝CB2＋CD2－2CB·CD·cosC＝52－48cosC，
∴20－16cosA＝52－48cosC解之：cosA＝－ ,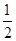
又0º＜A＜180º, ∴A＝120º，S＝16sin120º＝8
