问题
填空题
△ABC的三个角A<B<C，且２Ｂ＝Ａ＋Ｃ，最大边为最小边的2倍，则三内角之比为
.
答案
1:2:3
根据题意：△ABC的三个角A<B<C，且２Ｂ＝Ａ＋Ｃ，可得：B＝60º,且A＋C＝120º,又∵最大边为最小边的2倍，∴c=2a,∴据正弦定理可得：sinC=2sinA,将C＝120º－A代入该式可得：sin(120º-A)=2sinA,化简可得：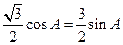
，故tanA=
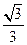,∴A=30º,C=90º,∴三角形三个内角之比为：A:B:C=1:2:3.