问题
填空题
设函数f(x)=
|
答案
∵函数f(x)=
,x2+1, x≤1 x2+x-2,x>1
∴f(-1)=(-1)2+1=2,
∴f[f(-1)]=f(2)=22+2-2=4,
故答案为:4.
设函数f(x)=
|
∵函数f(x)=
,x2+1, x≤1 x2+x-2,x>1
∴f(-1)=(-1)2+1=2,
∴f[f(-1)]=f(2)=22+2-2=4,
故答案为:4.
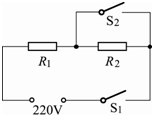
如表为一台电烤箱的铭牌,其内部简化电路如图所示,R1和R2均为电热丝.求:
| ××牌电烤箱 | ||
| 额定电压 | 220V | |
| 额定 功率 | 高温档 | 1100W |
| 低温档 | 440W | |
| 电源频率 | 50Hz | |
(2)当S1、S2闭合时,电烤箱处于什么档位?电路中R1的阻值是多少?
(3)电烤箱在低温档正常工作时,R1的功率是多少?