问题
选择题
△ABC中,a=x,b=2,B=45°,若三角形有两解,则x的取值范围是 ( )
A．x>2
B．x<2
C．2<x<2
D．2<x<2
答案
答案：C
考点：
分析：由题意判断出三角形有两解时，A的范围，通过正弦定理推出K的范围即可。
解：因为AC="b=2" 要使三角形有两解，就是要使以C为圆心，
半径为2的圆与BA有两个交点，
当A=90°时圆与AB相切；
当A=45°时交于B点，也就是只有一解．
所以45°＜A＜90°．即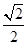
＜sinA＜1，
由正弦定理以及asinB=bsinA．可得：a=k=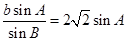
2sinA∈（2，2）．
所以 2＜x＜2．
教师点评:本题考查三角形的个数的判断方法，正弦定理的应用，考查计算能力