C  

题目分析：A、∵a=8，b=16，A=30°，∴由正弦定理得：sinB=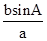=1，又B为三角形的内角，

∴B=90°，故只有一解，本选项不合题意；

B、∵a=30，b=25，A=150°，

∴由正弦定理得：sinB=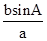=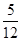，又A为钝角，∴B为锐角，

故只有一解，本选项不合题意；

C、∵a=72，b=50，A=135°，∴由正弦定理得：sinB==，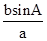

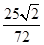又A为钝角，∴B为锐角，故只有一解，本选项不合题意；

D、∵a=30，b=40，A=26°，∴由正弦定理得：sinB==，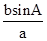

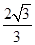∵a＜b，∴A＜B，即60°＜B＜180°，满足题意的B有两解，本选项符合题意，故选D。

事实上，由正弦定理，三角形ABC有两解的条件是，bsinA<a<b。

点评：简单题，判定三角形解的个数，往往利用正弦定理或结合图形进行分析。由正弦定理，三角形ABC有两解的条件是，bsinA<a<b。