问题
选择题
设△ABC的内角A，B，C所对的边分别为a，b，c.若三边的长为连续的三个正整数，且A＞B＞C，3b＝20acosA，则sinA∶sinB∶sinC为( )
A．4∶3∶2
B．5∶6∶7
C．5∶4∶3
D．6∶5∶4
答案
答案：D
因为a，b，c为连续的三个正整数，且A>B>C，可得
a＝c＋2，b＝c＋1 ①
又因为3b＝20acosA，由余弦定理可知cosA＝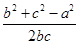
，则
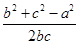3b＝20a· ②
联立①②，化简可得7c2－13c－60＝0，解得c＝4或c＝－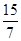
(舍去)，则a＝6，b＝5.
又由正弦定理可得，sinA∶sinB∶sinC＝a∶b∶c＝6∶5∶4.故选D.
