问题
解答题
在△ABC中，角A，B，C的对边分别为a，b，c，且bcosC=（3a-c）cosB，
（Ⅰ）求sinB的值；
（Ⅱ）若b=2，且a=c，求△ABC的面积。
答案
解：（Ⅰ）∵bcosC=（3a-c）cosB，
由正弦定理得sinBcosC=（3sinA-sinC）cosB，
∴sinBcosC+sinCcosB=3sinAcosB，
即sin（B+C）=3sinAcosB，sinA=3sinAcosB，
∵sinA＞0，sinB＞0，
∴
，
∴
。
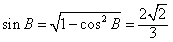（Ⅱ）由余弦定理得b2=a2+c2-2accosB，
而b=2，a=c，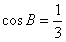
，
∴b2=2a2-2a2cosB=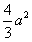
，
∴4=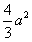
，a2=3，
∴
。