问题
解答题
有两个函数f(x)=asin(kx+
|
答案
由条件得
+2π k
=π k
π,∴k=2.3 2
由f(
)=g(π 2
),得a=2b①π 2
由f(
)=-π 4
g(3
)+1,得a=2-2b②π 4
∴由①②解得a=1,b=
.1 2
∴f(x)=sin(2x+
),g(x)=π 3
tan(2x-1 2
).π 3
∴当-
+kπ<2x-π 2
<π 3
+kπ,k∈Z时,g(x)单调递增.π 2
∴g(x)的单调递增区间为:(
-kπ 2
,π 12
+kπ 2
π)k∈Z.5 12

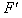 是力F1和F2合力的实际测量值
是力F1和F2合力的实际测量值 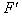 是F1和F2合力的理论值;F是力F1和F2合力的实际测量值
是F1和F2合力的理论值;F是力F1和F2合力的实际测量值