问题
解答题
在△ABC中,若sinA=2sinBcosC,且sin2A=sin2B+sin2C,试判断△ABC的形状。
答案
解:在△ABC中,
根据正弦定理: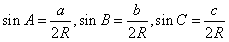 ,
,
∵sin2A=sin2B+sin2C,
∴a2=b2+c2,
∴△ABC是直角三角形且A=90°,
∴A=π-(B+C),sinA=2sinBcosC,
∴sin(B+C)=2sinBcosC,
∴sinBcosC-cosBsinC=0,即sin(B-C)=0,
∴B-C=0,即B=C,
∴△ABC是等腰直角三角形。
