问题
解答题
| 已知f(x)=x|x-a|-2 (1)当a=1时,解不等式
(2)当x∈[0,2]时,不等式f(x)<0恒成立,求实数a的取值范围. |
答案
(1)a=1时,
>0即f(x) x-3
>0,x|x-1|-2 x-3
∴
或 x≥1
>0x(x-1)-2 x-3 x<1
<0x(1-x)-2 x-3
∴1≤x<2 或x>3或x<1
∴x∈(-∞,2)∪(3,+∞)
(2)当x=0时,f(x)<0恒成立.
当x∈(0,2]时,x|x-a|-2<0.即x|x-a|<2.
∴x-
<a<x+2 x 2 x
令g(x)=x-
,h(x)=x+2 x
,x∈(0,2]2 x
则有g(x)max<a<h(x)min.
而g(x)=x-
,x∈(0,2]单增,故g(x)max=g(1)=1,2 x
又h(x)=x+
≥22 x
,故h(x)min=22 2
所以a∈(1,2
)2

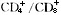 >3.5,血沉增快,血钙增高,最可能的诊断是()
>3.5,血沉增快,血钙增高,最可能的诊断是()