问题
填空题
在△ABC中,a=5,b=4,cos(A-B)=
|
答案
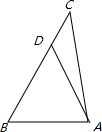
∵a>b,∴A>B.在BC上取D,使得BD=AD,连接AD,
设BD=x,则AD=x,DC=5-x.
在△ADC中,注意cos∠DAC=cos(A-B)=
,31 32
由余弦定理得:(5-x)2=x2+42-2x•4•
,31 32
即:25-10x=16-
x,31 4
解得:x=4.
∴在△ADC中,AD=AC=4,CD=1,
∴cosC=
=
CD1 2 AC 1 8
故答案为:1 8
