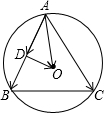
问题
填空题
已知O是锐角△ABC的外接圆圆心,∠A=θ,若
|
答案
取AB中点D,则有
=AO
+AD
,DO
代入cosB sinC
+AB cosC sinB
=2mAC
得:AO
cosB sinC
+AB cosC sinB
=2m(AC
+AD
),DO
由
⊥OD
,得AB
•DO
=0,AB
∴两边同乘
,化简得:AB
cosB sinC
•AB
+AB cosC sinB
•AC
=2m(AB
+AD
)•DO
=mAB
•AB
,AB
即
c2+cosB sinC
bc•cosA=mc2,cosC sinB
由正弦定理
=a sinA
=b sinB
化简得:c sinC
sin2C+cosB sinC
sinBsinCcosA=msin2C,cosC sinB
由sinC≠0,两边同时除以sinC得:cosB+cosAcosC=msinC,
∴m=
=cosB+cosAcosC sinC -cos(A+C)+cosAcosC sinC
=
=sinA,-cosAcosC+sinAsinC+cosAcosC sinC
又∠A=θ,
则m=sinθ.
故答案为:sinθ