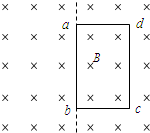
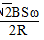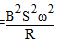问题
解答题
| 在△ABC中,角A,B,C的对边分别为a,b,c. (1)若a=2
(2)若a=2,A=
(3)设
|
答案
(1)∵a=2
,b=c=2,3
∴由余弦定理得:cosA=
=b2+c2-a2 2bc
=-4+4-12 8
,1 2
又A为三角形的内角,
则A=
;…(4分)2π 3
(2)∵A=
,B=π 3
,则C=5π 12
,…(6分)π 4
∴sinA=
,sinC=3 2
,又a=2,2 2
∴由正弦定理得:
=2 3 2
,c 2 2
∴c=
;…(8分)2 6 3
(3)∵
=(cosA,cos2A),m
=(-n
, 1),12 5
∴
•m
=-n
cosA+cos2A=-12 5
cosA+2cos2A-1=2(cosA-12 5
)2-3 5
,…(10分)43 25
∴当cosA=
时,3 5
•m
取最小值,n
又A为三角形的内角,
∴sinA=
=1-cos2A
,4 5
∴tanA=
,…(13分)4 3
则tan(A-
)=π 4
=tanA-1 1+tanA
=
-14 3 1+ 4 3
.…(15分).1 7

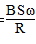 cosωt
cosωt