若u=f(xyz),f(0)=0,f’(1)=1,且
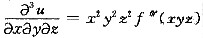 ,求u.
,求u.
参考答案:[详解] 因为[*]
故 3xyzf"(xyz)+f’(xyz)=0.
令 xyz=t,即3tf"(t)+f’(t)=0.
设 υ=f’(t),得3tυ’+υ=0及[*]从而[*]
因为f(0)=0,所以C=0.于是[*],即[*]
解析:
[分析]: 对函数u=f(xyz)按次序求高阶偏导[*]代入已知式,可令xyz=t得t的微分方程解之.
[评注] 本题综合考查了多元函数求偏导与微分方程的求解问题.利用偏导数引出微分方程是一类典型的命题考查的情形.
