问题
问答题
设二次型f(x1,x2,x3)=xTAx=
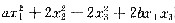 (b>0)
(b>0)
其中二次型矩阵A的特征值之和为1,特征值之积为-12.
(1)求a,b的值;
(2)利用正交变换将二次型f化为标准形,并写出所用的正交变换和对应的正交矩阵.
答案
参考答案:[详解] (1)二次型f的矩阵为
[*]
设A的特征值为λi(i=1,2,3),由题设,有
∑λi=a+2+(-2)=1;
∏λi=|A|=2(-2a-b2)=-12.
解出a=1,b=2.(已知b>0).
(2)由矩阵A的特征多项式
[*]
=(λ-2)2(λ+3),
解出A的特征值λ1=λ2=2,λ3=-3.
对λ=2,由(2E-A)X=0,即
[*]
得基础解系α1=(0,1,0)T,α2=(2,0,1)T,即λ=2的线性无关的特征向量.对λ=-3,由(-3E-A)X=0,即
[*]
得基础解系α3=(1,0,-2)T,即λ=-3的特征向量.
由于α1,α2已正交,故只需单位化,有
γ1=(0,1,0)T,[*]
那么,令 [*]
则在正交变换x=Py下,二次型f有标准形.
f(x1,x2,x3)=xTAx=yTAy=[*]
