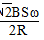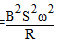问题
解答题
化简:
|
答案
=(1+sinα+cosα)(sin
-cosα 2
)α 2 2+2cosα
=(1+2sin
cosα 2
+2cos2α 2
-1)(sinα 2
-cosα 2
)α 2 2+2(2cos2
-1)α 2
=2cos
(sinα 2
+cosα 2
)(sinα 2
-cosα 2
)α 2 2|cos
|α 2
.2cos
(-cosα)α 2 2|cos
|α 2
再由 π<α<2π,可得
<π 2
<π,∴cosα 2
<0,2|cosα 2
|=-2cosα 2
.α 2
故原式=
=cosα.2cos
(-cosα)α 2 2|cos
|α 2

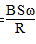 cosωt
cosωt