问题
问答题
设x0＞0，
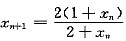(n=0，1，2，…)
(1)证明：1＜xn＜2；
(2)求
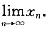
答案
参考答案：[详解] (1)x0＞0，则[*]n，xn＞0．
因为 [*]
又因为 [*]
所以 [*]n≥1时，1＜xn＜2．
(2)[*]
即xn+1-xn和xn-xn-1有相同的正负号．
∴当x1＞x0时{xn}单增；
当x1＜x0时{xn}单减．
因为1＜xn＜2 (n=1，2，…)，
所以{xn}总是单调有界数列，
所以 [*]=A存在．
[*]
即 [*]
解析：
[分析]： 凡是用递推公式出现的数列，一般要使用定理：单调有界数列一定有极限．
[评注] 应注意到本题中{xn}的单调性和x1的取值有关，但由1＜xn＜2知，任何情形，{x0