问题
问答题
三阶实对称矩阵的三个特征值为λ1=6，λ2=λ3=3，对应于λ2=λ3=3的特征向量为
，
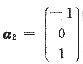，求对应于λ1=6的特征向量及矩阵A．
答案
参考答案：[详解] 设λ1=6对应的特征向量为α1=(x1，x2，x3)T，
∴α1⊥α2，α1⊥α3，
[*]
令[*]
则[*]
解析：
[分析]： 设λ1对应的特征向量为α1，对于实对称矩阵，不同特征值的特征向量正交，所以α1⊥α2，α1⊥α3．
[评注] 本题也可将α1,α2，α3标准化(α2，α3已经是正交向量)得正交矩阵Q，则[*]