问题
问答题
设f(x)在x=0点处连续，且
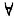x1，x2∈(-∞，+∞)有f(x1+x2)=f(x1)+f(x2)，证明y=f(x)在(-∞，+∞)上连续．
答案
参考答案：[详解] 令x1=x2=0，则f(0)=2f(0)，∴f(0)=0．
任取x0∈(-∞，+∞)，
[*]
∴y=f(x)在x=x0连续．
由x0的任意性知y=f(x)在(-∞，+∞)连续．
解析：
[分析]： 由f(x1+x2)=f(x1)+f(x2)，取特殊的x1，x2可算出某些函数值，该题中取x1=x2=0，可算出f(0)=0．
[评注] 连续性有两个定义：
[*]
第一个定义经常用于证明题，第二个定义经常用于计算题．