问题
问答题
(1)设X1，X2，…，Xn是取自总体X～N(μ，σ2)的一组简单随机样本，试证
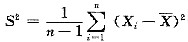是σ2的一致估计量．
(2)设X1，X2，…，X25是取自于正态总体N(μ，9)的一组简单随机样本，其中μ为未知参数，如果对检验问题H0:μ=μ0，H1:μ≠μ0，取检验的拒绝域为ω=(x1，x2，…，x25):|
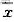-μ0|≥C，其中
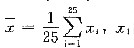，x1，x2，…，x25为样本观测值．试决定常数C，使检验的显著性水平为0.05．
答案
参考答案：[详解] (1)由于[*]，并且有
E(S2)=σ2，[*]
[*]
根据切比雪夫不等式有：
[*]
即得[*]
可见S2是σ2的一致估计量．
(2)因为X～N(μ，9)，所以[*]
在H0成立下，[*]
即，[*]
所以C=1.176．
解析：
[分析]： (1)一致性的证明一般用切比雪夫不等式；
(2)假设检验的统计量为：[*]
[评注] 由(1)知[*]是总体X的一致、无偏估计量，但不一定是有效估计量．
