问题
填空题
若
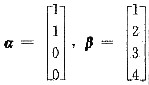，A=αβ1，B是4阶矩阵，r(B) =2，则r(AB-2B)=______．
答案
参考答案：B
解析：
[分析]： r(AB-2B)=r[(A-2E)B]．若A-2E可逆，则r(AB-2B)=r(B)．
[详解] AB-2B=(A-2E)B．而
[*]
显然 |A-2E|=-8≠0．
从而A-2E可逆，故r((A-2E)B)=r(B)=2．
[评注] 一般地，若r(Am×n=n，则r(AB)=r(B)；若r(Bn×s)=n，则r(AB)=r(A)．