设函数f（x）是定义在R上的奇函数，在(12，1)上单调递增，且满足_爱下问搜题

搜题请搜索小程序“爱下问搜题”

问题填空题

设函数f（x）是定义在R上的奇函数，在(

1

2

，1)上单调递增，且满足f（-x）=f（x-1），给出下列结论：①f（1）=0；②函数f（x）的周期是2；③函数f（x）在(-

1

2

，0)上单调递增；④函数f（x+1）是奇函数．
其中正确的命题的序号是______．

答案

①∵函数f（x）是定义在R上的奇函数

∴f（0）=0，

又∵f（-x）=f（x-1）

∴f（-1）=f（1）=0

正确．

②∵奇函数和f（-x）=f（x-1），

∴f（x-1）=-f（x），

∴f（x+2）=f（x）

∴函数f（x）的周期是2．

③由②知无法得知其性质，不正确．

④∵函数f（x+1）的图象是由f（x）的图象向左平移1个单位，

∵f（x）是奇函数，f（x-1）=-f（x），

∴f（1-x）=f（x），

即函数f（x）关于x=

1

2

对称，可得出（1，0）点也是对称中心

所以f（x+1）是奇函数，正确．

故答案为：①②④

选择题

下列各项中，不属于生物的是：（　　）

A．变形虫

B．石笋

C．地衣

D．细菌

问答题

打开工作簿文件EX04．XLS(内容如下)，将工作表Sheetl的A1：C1单元格合并为一个单元格，内容居中，计算“人数”列“总计”行及“所占百分比”列(“所占百分比”字段为“百分比”型(小数点后位数为2)，所占百分比；人数/总计)，将工作表命名为“师资情况表”。

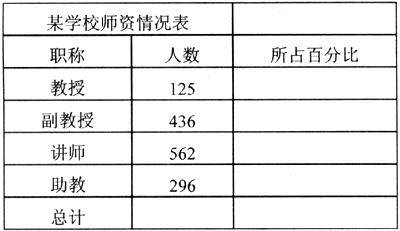(2)选取“师资情况表”的“职称”和“所占百分比”两列单元格的内容建立“分离型圆环图”(系列产生在“列”)，数据标志为“显示百分比”，标题为“师资情况图”，插入到表的A9：D19单元格区域内。