问题
解答题
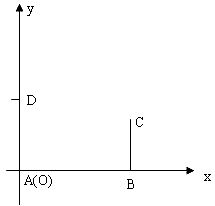
铁路上AB两点相距25千米，CD为两村庄，DA垂直AB于A，CB垂直AB于B，已知DA=15千米，CB=10千米。以A点为原点，AB所在的直线为X轴，DA所在的直线为Y轴建立直角坐标系。
（1）现在要在铁路AB上建一个收购站E，使得C、D两村到E站的距离相等。在图中画出E点，并求出E点的坐标。
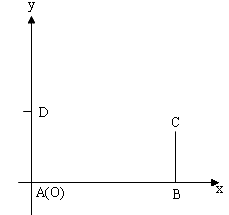
（2）若还要在AB建一个供应站F，使得F点到C、D两村的距离之和最短。找出F点的位置,并求出F点的坐标。
答案
解：（1）图“略”
设AE=x，则BE=25-x ，在直角三角形ADE和CBE中，
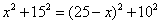解得x=10 E(10，0)
（2）图“略”
D(0, 15)关于x轴的对称点是D1（0，-15），设直线CD1的解析式是y=kx+b(k≠0)，则
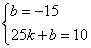
∴y=x-15 令y=0，则x=15 所以F点（15，0）