问题
证明题
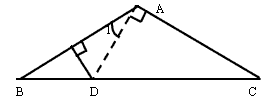
已知：如图△ABC中，AB=AC，∠A=120°。AB边后垂直平分线交BC于D，求证：DC=2BD。
答案
证明：连结AD ∵D在AB垂直平分线上
∴BD=AD ∴∠B=∠1
∵∠BAC=120° AB=AC
∴∠B=∠C=30° ∴∠DAC=90°
在Rt△DAC中
∵∠C=30°∴DC=2AD ∴DC=2BD
搜题请搜索小程序“爱下问搜题”
已知：如图△ABC中，AB=AC，∠A=120°。AB边后垂直平分线交BC于D，求证：DC=2BD。
证明：连结AD ∵D在AB垂直平分线上
∴BD=AD ∴∠B=∠1
∵∠BAC=120° AB=AC
∴∠B=∠C=30° ∴∠DAC=90°
在Rt△DAC中
∵∠C=30°∴DC=2AD ∴DC=2BD