问题
解答题
| 解不等式(组),并将解集在数轴上表示出来 (1)
(2)
(3)
(4)
|
答案
(1)原不等式的两边同时乘以4,得
4x-2-5x+1<0,即-x-1<0,
移项,得
-x<1,
不等式的两边同时除以-1(不等号的方向发生改变),得
x>-1,即原不等式的解集是x>-1;

(2)由不等式
-2x-1 3
≤1,得5x+1 2
4x-2-15x-3≤6,
移项、合并同类项,得
-11x≤11,即x≥-1;
由不等式5x-1<3(x+1),得
2x<4,即x<2;
所以,原不等式组的解集是-1≤x<2;

(3)原不等式的两边同时乘以6,得
2x+6>21-3x,
移项、合并同类项,得
5x>15,
不等式的两边同时除以5,得
x>3,即原不等式的解集是x>3;
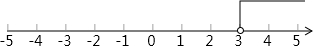
(4)由不等式x-3(x-2)≥4,得
-2x≥-2,即x≤1;
由不等式
>x-1,得1+2x 3
1+2x>3x-3,
移项、合并同类项,得
4>x,即x<4;
所以,原不等式组的解集是x<4;

