问题
证明题
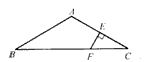
如图所示，已知在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F，
求证：BF=2CF。
答案
证明：连结AF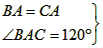
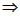∠C=∠B=30°
EF是AC的垂直平分线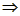
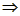FA=FC∠FAC=∠C=30°，
∴∠BAF =90°而∠ABF＝30°，
∴BF=2AF=2CF。
搜题请搜索小程序“爱下问搜题”
如图所示，已知在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F，
求证：BF=2CF。
证明：连结AF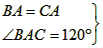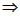∠C=∠B=30°
EF是AC的垂直平分线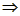FA=FC∠FAC=∠C=30°，
∴∠BAF =90°而∠ABF＝30°，
∴BF=2AF=2CF。