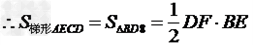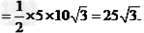问题
解答题
在四边形ABCD中,AD∥BC,AB=DC,AC与BD相交于O,∠BOC=120°,AD=7,BD=10,求四边形ABCD的面积。
答案
解:(1)当AD=BC时,如图1,
四边形ABCD为平行四边形,
∴BC=AD=7,BO=5,过B作BE⊥AC于E,∠BOE=60°
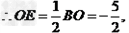
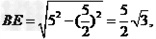
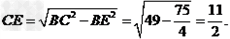
∴ OC= CE-OE=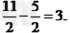
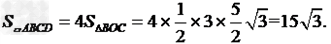

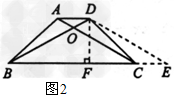
(2)当AD≠BC时,如图2.
四边形ABCD为等腰梯形,过点D作DE∥AC交BC的延长线于点E,作DF⊥BE于点F.
则∠BDE=∠BOC=120°∠DBE=∠E=30°
∴ DF= 5,BF=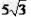
∴BE= 2BF=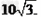
而四边形ACED为平行四边形,
∴AD= CE,