某同学在“利用单摆测定重力加速度”的实验中,测得摆线长为L,摆球直径为d,然后用秒表测得n次全振动的时间为t,则:
(1)重力加速度的表达式g=______.(用上述符号表示)
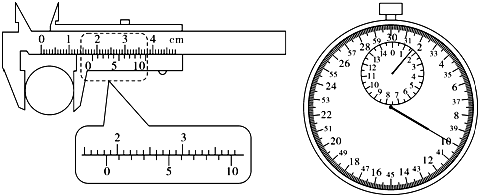
(2)若用最小分度为毫米的刻度尺测得摆线长为970.8mm,用10分度的游标卡尺测得摆球直径如图,摆球的直径为______mm.单摆在竖直面内摆动,用秒表测出单摆做50次全振动所用的时间如图,则t=______s,单摆的周期为______s.求得当地的重力加速度为______m/s2.(取π2=10)
(3)如果他测得的g值偏小,可能的原因是______
A、测摆线长时摆线拉得过紧
B、摆球在水平面内做圆周运动
C、摆线上端悬点未固定,振动过程中出现松动,摆线长度增加了
D、开始计时,秒表过迟按下.
(1)单摆摆长l=L+
,单摆周期T=d 2
,由单摆周期公式T=2πt n
可知,l g
g=
=4π2l T2
=4π2(L+
)d 2 (
)2t n
;4π2n2(L+
)d 2 t2
(2)由图示游标卡尺可知,主尺的示数是18mm,游标尺的示数是4×0.1mm=0.4mm,
则游标卡尺示数,即小球直径d=18mm+0.4mm=18.4mm;
由图示秒表可知,分针示数是1m=60s,秒针示数是40s,秒表示数是60s+40s=100.0s,单摆周期T=
=t n
=2.0s;100s 50
单摆摆长l=L+
=970.8mm+d 2
=980mm=0.98m,重力加速度g=18.4mm 2
=4π2l T2
=9.8m/s2;4×10×0.98 22
(3)由g=
=4π2l T2
可知:4π2n2(L+
)d 2 t2
A、测摆线长时摆线拉得过紧,摆长偏大,所测重力加速度偏大,不符合题意;
B、摆球在水平面内做圆周运动,成为圆锥摆,摆的摆长为(L+
)cosθ,d 2
θ是摆的偏角,单摆摆长偏小,所测重力加速度偏小,符合题意;
C、摆线上端悬点未固定,振动过程中出现松动,摆线长度增加了,所测重力加速度偏大,不符合题意;
D、开始计时,秒表过迟按下,所测时间t偏小,所测重力加速度偏大,不符合题意;
如果他测得的g值偏小,可能的原因是:B、摆球在水平面内做圆周运动;
故答案为:(1)
(L+4n2π2 t2
);(2)18.4;100.0;2.0;9.8;(3)B.d 2
