问题
问答题
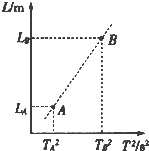
某同学利用单摆测定当地重力加速度,发现单摆静止时摆球重心在球心的正下方,他仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两个点.坐标如图所示,他采用恰当的数据处理方法,则计算重力加速度的表达式应为g=______.请你判断该同学得到的实验结果与摆球重心就在球心处的情况相比,将______.(填“偏大”、“偏小”或“相同”)
答案
由单摆周期公式T=2π
可知,l=l g
T2,则k=g 4π2
,g=4π2k;g 4π2
由图象可知,图象的斜率k=
,则g=LB-LA
-T 2B T 2A
;4π2(LB-LA)
-T 2B T 2A
由l=
T2=kT2,l与T2成正比,k=g 4π2
是比例常数,由图象可知l与T2成正比,由于单摆摆长偏大还是偏小不影响图象的斜率k,因此摆长偏小不影响重力加速度的测量值,用图线法求得的重力加速度准确,该同学得到的实验结果与摆球重心就在球心处的情况相比,将相同.g 4π2
故答案为:
,相同.4π2(LB-LA)
-T 2B T 2A
