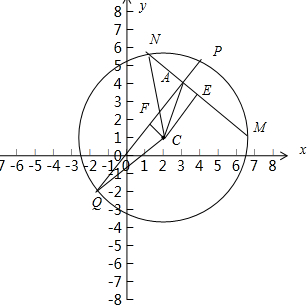圆C的方程为（x-2）²+（y-1）²=25，

圆心坐标C（2，1），半径R=5

设弦MN，PQ的中点分别为E，F，

则CE²+CF²=CA²=（3-2）²+（4-1）²=10，

CE²+NE²=CF²+QF²=25，

NE²+QF²=（25-CE²）+（25-CF²）=50-（CE²+CF²）=40，

MN²+PQ²=4（NE²+QF²）=160

∴S²=

1

4

MN²×PQ²=

1

4

MN²×（160-MN²），

MN²∈[60，100]．

当MN²=80时，S²取得最大值：S₁²=1600．

当MN²=60时，S²取得最小值：S₂²=1500．

则

S

21

-

S

22

=1600-1500=100

故选：B．