问题
计算题
解不等式 ｜x-5｜-｜2x+3｜＜1
答案
解：（1）当x≤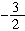
时，原不等式化为-（x-5）-［-（2x+3）］＜1， 解得x<-7，结合x≤
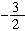，故x<-7是原不等式的解；
（2）当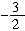
＜x≤5时，原不等式化为 -（x-5）-（2x+3）＜1，
解得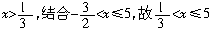
是原不等式的解；
（3）当x＞5时，原不等式化为： x-5-（2x+3）＜1， 解得x＞-9，结合x＞5，故x＞5是原不等式的解。
综合（1），（2），（3）可知
，是原不等式的解。