问题
解答题
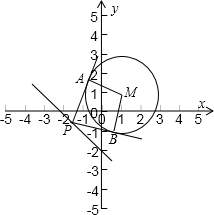
已知圆M过两点C（1，-1）、D（-1，1）且圆心M在直线x+y-2=0上．
（1）求圆M的方程；
（2）设P是直线3x+4y+8=0上的动点，PA、PB是圆M的两条切线，A、B为切点，求四边形PAMB的面积的最小值．
答案
（1）设圆M的方程为：（x-a）2+（y-b）2=r2（r＞0），
根据题意得
，解得：a=b=1，r=2，(1-a)2+(-1-b)2=r2 (-1-a)2+(1-b)2=r2 a+b-2=0
故所求圆M的方程为：（x-1）2+（y-1）2=4；
（2）由题知，四边形PAMB的面积为S=S△PAM+S△PBM=
（|AM||PA|+|BM||PB|）．1 2
又|AM|=|BM|=2，|PA|=|PB|，所以S=2|PA|，
而|PA|2=|PM|2-|AM|2=|PM|2-4，
即S=2
．|PM|2-4
因此要求S的最小值，只需求|PM|的最小值即可，即在直线3x+4y+8=0上找一点P，使得|PM|的值最小，
所以|PM|min=
=3，所以四边形PAMB面积的最小值为23+4+8 5
=2|PM|2-4
．5
