问题
填空题
平行四边形ABCD中，E是BC中点，F是BE中点，AE与DF交于H，则AH：HE=______．
答案
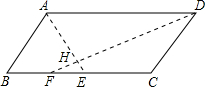
∵E是BC中点，F是BE中点，
∴EF=
BC=1 4
AD，1 4
∵平行四边形ABCD中，
∴∠DAH=∠FEH，∠ADH=∠EFH，
∴△DAH∽△FEH，
∴
=AH EH
=4，AD EF
即AH：HE=4．
故答案为：4．
搜题请搜索小程序“爱下问搜题”
平行四边形ABCD中，E是BC中点，F是BE中点，AE与DF交于H，则AH：HE=______．
∵E是BC中点，F是BE中点，
∴EF=
BC=1 4
AD，1 4
∵平行四边形ABCD中，
∴∠DAH=∠FEH，∠ADH=∠EFH，
∴△DAH∽△FEH，
∴
=AH EH
=4，AD EF
即AH：HE=4．
故答案为：4．