问题
解答题
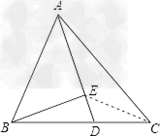
如图，△ABC中，点E是AB，BC的垂直平分线的交点，AE的延长线交BC于点D，AB=AD，AE=BD。
①求证：AB=BC；
②求∠DAC的度数．
答案
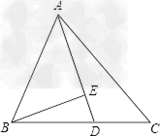
解：（1）连接CE
∵点E是AB，BC的垂直平分线的交点，
∴AE=BE=CE，
∵∠EAB=∠EBA，∠EBD=∠ECB，∠EAC=∠ECA
∴AE=BD，
∴BE=BD，
∴∠BED=∠BDE
又∵AB=AD，
∴∠ABD=∠BDE，
∴∠BED=∠ABD
∵∠BED=∠EAB+∠ABE，∠ABD=∠ABE+∠DBE，
∴∠EAB=∠EBD
又∵∠EAB=∠EBA，∠EBD=∠ECB，
∴∠EAB=∠ECB，
∴∠EAC+∠EAB=∠ECB+∠ECA，即∠BAC=∠BCA，
∴AB=BC；
（2）设∠BAD=x，
∵AE=BE，
∴∠AEE=x，
∵∠BED是△ABE的外角，
∴∠BED=2x，
∵BE=BD，
∴∠ADB=∠BED=2x，
∵AB=AD，
∴∠ABD=2x，
∴∠BAD+∠ABD+∠ADB=x+2x+2x=180°，解得x=36°，
∴∠ABD=72°，
∵AB=BC，
∴∠BAC=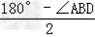
=
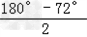=54°，
∴∠DAC=∠BAC-∠BAD=54°-36°=18°。
