问题
填空题
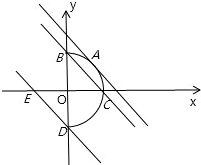
直线y=-x-b与曲线x=
|
答案
由题意可知:曲线方程表示一个在y轴右边的单位圆的一半,
则圆心坐标为(0,0),圆的半径r=1,
当直线y=-x-b与圆相切时,
圆心到直线的距离d=
=r=1,解得b=-|-b| 2
;2
当直线在直线ED与直线BC之间时,直线y=-x-b与直线ED重合时,b=1,与直线BC重合时,b=-1,
所以-1<b≤1,
综上,b的取值范围为-1<b≤1或b=-
.2
故答案为:-1<b≤1或b=-2