∵⊙P：（x-2）²+（y-2）²=18，

∴圆心P（2，2），半径r=

18

=3

2

．

要使⊙P上恰好有三个不同的点到直线l：ax+by=0的距离为2

2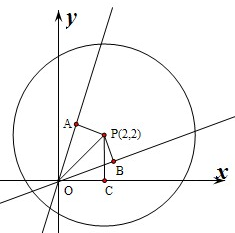

，

则圆心P到直线ax+by=0的距离为3

2

-2

2

=

2

即可．

如图：则AP=BP=

2

，

∵圆心P（2，2），

∴OP=2

2

，

则∠POC=

π

4

，

∵AP=BP=

2

，OP=2

2

，

∴在直角三角形OAP和OBP中，

sin∠AOP=sin∠BOP=

2

2 2

=

1

2

，

∴∠AOP=∠BOP=

π

6

，

∴l的倾斜角为∠AOC或∠BOC，

∴∠AOC=

π

4

+

π

6

=

5π

12

或∠BOC=

π

4

-

π

6

=

π

12

．

故选：D．