I.一矿区的重力加速度偏大,某同学“用单摆测定重力加速度”实验探究该问题.]
(1)用最小分度为毫米的米尺测得摆线的长度为990.8mm,用10分度的游标卡尺测得摆球的直径如图1所示,摆球的直径为______mm.
(2)把摆球从平衡位置拉开一个小角度由静止释放,使单摆在竖直平面内摆动,用秒表测出单摆做50次全振动所用的时间,秒表读数如图2所示,读出所经历的时间,单摆的周期为______s.
(3)测得当地的重力加速度为______m/s2.(保留3位有效数字)
II.一块电流表的内阻大约是几百欧,某同学用如图3电路测量其内阻和满偏电流,部分实验步骤如下:
①选择器材:两个电阻箱、2节干电池(每节电动势为1.5V,内阻不计)、2个单刀单掷开关和若干导线;
②按如图3所示的电路图连接好器材,断开开关S1、S2,将电阻箱1的电阻调至最大;
③闭合开关S1,调节电阻箱1,并同时观察电流表指针,当指针处于满偏刻度时,读取电阻箱1的阻值为500Ω;
④保持电阻箱1的电阻不变,再闭合开关S2,只调节电阻箱2,并同时观测电流表指针,当指针处于半偏刻度时,读取电阻箱2的阻值为250Ω.
通过分析与计算可知:
(1)电流表内阻的测量值 RA=______;电流表的满偏电流值 Ig=______;
(2)该同学发现电流表满偏刻度的标称值为“3A”,与测量值完全不符.于是将一个电阻箱与电流表并联进行改装,使改装后的电流表量程与满偏刻度的标称值相符,则改装后的电流表的内阻
=_______.R /A
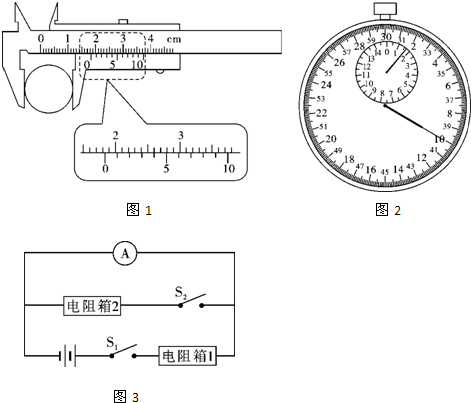
Ⅰ(1)由图1所示游标卡尺可知,主尺示数是1.8cm=18mm,
游标尺示数是4×0.1mm=0.4mm,游标卡尺示数,即摆球的直径为18mm+0.4mm=18.4mm;
(2)由图2所示秒表可知,分针示数是1min=60s,秒针示数是40s,则秒表示数是60s+40s=100s,
单摆周期T=
=t n
=2s;100s 50
(3)单摆摆长L=l+
=990.8mm+d 2
=1000mm=1m;18.4mm 2
由单摆周期公式T=2π
,可知重力加速度:g=L g
=4π2L T2
≈9.86m/s2;4×(3.14)2×1m (2s)2
Ⅱ(1)由题意知电源电动势E=1.5V×2=3V;
闭合开关S1,断开S2时,电阻箱1与电流表串连接入电路,
当指针处于满偏刻度时,读取电阻箱1的阻值为500Ω,
由串联电路特点及欧姆定律可得:E=Ig(RA+R1),即:3V=Ig(RA+500Ω) ①,
闭合开关S1、S2时,电流表与电阻箱2并联,然后与电阻箱1串联,
电阻箱1阻值不变,电流表指针处于半偏刻度,电阻箱2的阻值为250Ω,
此时电流表两端电压为:UA=IARA=
×RA,流过电阻箱2的电流:Ig 2
I2=
=U2 R2
=UA R2
=IgRA 2 R2
=IgRA 2×250Ω
,干路电流I=IA+I2=IgRA 500Ω
+Ig 2
,IgRA 500Ω
由串联电路特点及欧姆定律可得:E=+UA+U1=
+IR1═IgRA 2
+(IgRA 2
+Ig 2
)R1,IgRA 500Ω
即3V═
+(IgRA 2
+Ig 2
)×500Ω ②,IgRA 500Ω
由①②解得:RA=500Ω,Ig=0.003A=3mA;
(2)电流表的满偏电压UA=IgRA=0.003A×500Ω=1.5V,
改装后电流表的内阻RA′=
=UA Ig′
=0.5Ω.1.5V 3A
故答案为:I、(1)18.4;(2)2.0;(3)9.86;
II、(1)500Ω;(2)3mA;(3)0.5Ω.
