问题
解答题
已知直线l：x=4与x轴相交于点M，动点P满足PM⊥PO（O是坐标原点）．
（1）求动点P的轨迹C的方程；
（2）试在直线l上确定一点D（异于M点），过点D作曲线C的切线，使得切点E恰为切线与x轴的交点F与点D的中点．
答案
解：（1）依题意，M（4，0）
设P（x，y）（x≠0且x≠4），
由PM⊥PO，得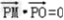
，
即x（x﹣4）+y2=0
整理得：动点P的轨迹C的方程为（x﹣2）2+y2=4（x≠0且x≠4）
（2）因为DE、DM都是圆（x﹣2）2+y2=4的切线，所以DE=DM
因为E点是DF的中点，所以DF=2DE=2DM，
所以∠DFN=
设C（2，0），
在△CEF中，∠CEF=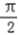
，∠CFE=
，CE=2，
所以CF=4，FM=6
从而DM=2
，
故D（4，±2
）