问题
解答题
| 在平面直角坐标系xOy中,曲线y=x2+2x-3与坐标轴的交点都在圆C上. (Ⅰ)求圆C的方程; (Ⅱ)若圆C被直线x-y+a=0截得的弦长为2
|
答案
(I)曲线y=x2-2x-3与y轴的交点为A(0,-3),与x轴的交点为B(1,0)、D(-3,0).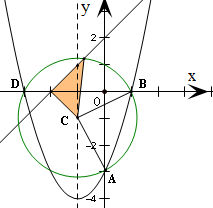
∵线段BD的垂直平分线为x=-1,
∴设圆C的圆心为(-1,b),
由|AC|=|BC|,得(0+1)2+(-3-b)2=(1+1)2+b2,解得b=-1.
由此可得圆心C(-1,-1),
圆C的半径r=
=(1-0)2+(-1+3)2
,5
因此,圆C的方程为(x+1)2+(y+1)2=5.
(II)∵直线x-y+a=0被圆C截得的弦长为2
,3
∴设点C到直线x-y+a=0的距离为d,
根据垂径定理得2
=2r2-d2
,3
即
=5-d2
,解得d=3
(舍负).2
∴点C(-1,-1)到直线x-y+a=0的距离为
=|-1+1+a| 2
,2
解得a=±2.
