问题
解答题
自点A(-3,3)发出的光线l射到x轴上被x轴反射,其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,求反射光线所在直线的方程。
答案
解:点A(-3,3)关于x轴的对称点为B(-3,-3),
反射线所在直线过点B,设其方程为y+3=k(x+3),即kx-y+3k-3=0,
圆x2+y2-4x-4y+7=0的方程可化为(x-2)2+(y-2)2=1,
∵反射线所在直线与圆相切,∴ ,
,
解得:k=或k=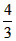 ,
,
∴所求直线方程为:3x-4y-3=0或4x-3y+3=0。