问题
解答题
已知圆x2+y2-4x+2y-3=0和圆外一点M（4，-8），
（Ⅰ）过M作圆的切线，切点为C、D，求切线长及CD所在直线的方程；
（Ⅱ）过M作圆的割线交圆于A，B两点，若|AB|=4，求直线AB的方程。
答案
解：（Ⅰ）圆即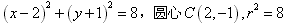
，
切线长为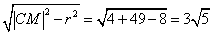
，
CD直线方程为：2x-7y-19=0。
（Ⅱ）①若割线斜率存在，设AB：y+8=k（x-4），即kx-y-4k-8=0，
设AB中点为N，
则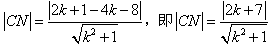
，
由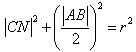
，得
；
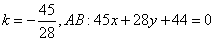②若割线斜率不存在，AB：x=4，
代入圆方程，
设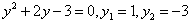
符合题意；
总之，AB：45x+28y+44=0或x=4。