问题
解答题
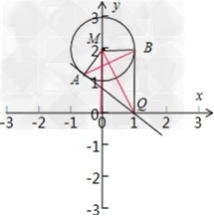
已知圆M：x2+（y﹣2）2=1，Q是x轴上的动点，QA、QB分别切圆M于A，B两点
（1）求四边形QAMB的面积的最小值
（2）若点Q的坐标为（1，0），求切线QA、QB及直线AB的方程．
答案
解：（1）圆M：x2+（y﹣2）2=1，Q是x轴上的动点，QA、QB分别切圆M于A，B两点
∴MA⊥AQ，MA=1．
∴SQAMB=2S△AQB=MA·QA=QA= 
=
≥
=
．
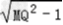（2）点Q的坐标为（1，0），
设过点Q的圆的切线方程为x=my+1，
则圆心M到切线x﹣my﹣1=0的距离为1．
∴ 
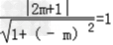即 
解得m=0或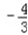
．
∴切线QA、QB的方程分别为3x+4y﹣1=0和x=1．切点B（1，2），
∵AB⊥MQ，所以KAB=﹣
=﹣
= 
．
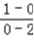所以AB的方程为：y﹣2= （x﹣1）．即x﹣2y+3=0．
