问题
证明题
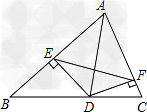
如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，求证：AD垂直平分EF．
答案
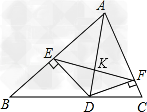
证明：设AD、EF的交点为K，
∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE=DF．
∴D在线段EF的垂直平分线上．
∵DE⊥AB，DF⊥AC，
∴∠AED=∠AFD=90°，
在Rt△ADE和Rt△ADF中，
AD=AD，DE=DF，
∴Rt△ADE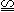
Rt△ADF（HL）．
∴AE=AF．
又∵∠EAD=∠FAD，AK=AK，
∴△AE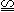K
△AFK，
∴EK=KF，∠AKE=∠AKF=90°，
∴AD是线段EF的垂直平分线．
选择题
