问题
解答题
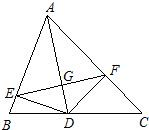
如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF.
答案
证明:由AD是∠BAC的平分线,可得∠EAD=∠FAD,
又∵∠DEA=∠DFA=90°,AD为公共边,
∴可证得△AED≌△AFD.
∴AE=AF,可知△AEF为等腰三角形.
由AE=AF,AG为公共边,∠EAD=∠FAD,
∴△AEG≌△AFG(SAS).
∴可得EG=FG.
∴AG是△AEF的中线.
又∵等腰三角形的三线合一,
∴AD垂直平分EF.
