问题
解答题
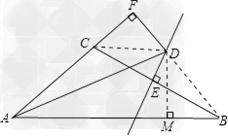
已知:如图,△ABC中,∠A的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF垂直于AC交AC的延长线于点F.求证:AB﹣AC=2CF.

答案
解:证明:连接CD,DB,作DM⊥AB于一点M,
∵AD平分∠A,DF⊥AC,DM⊥AB,
∴DF=DM(角平分线上的点到角的两边距离相等)
∵AD=AD,
∠AFD=∠AMD=90°,
∴△AFD≌△AMD,
∴AF=AM,
∵DE垂直平分线BC,
∴CD=BD(垂直平分线上的点到线段两端点距离相等),
∵FD=DM,∠AFD=∠DMB=90°,
∴Rt△CDF≌Rt△BDM,
∴BM=CF,
∵AB=AM+BM,AF=AC+CF,AF=AM,BM=CF,
∴AB=AC+2CF,
∴AB﹣AC=2CF.