(1)在“利用单摆测重力加速度”的实验中,测得单摆的摆角小于5°,完成n次全振动的时间为t,用毫米刻度尺测得的摆线长为L,用五十分度的游标卡尺测得摆球的直径d.
①用上述物理量的符号写出求重力加速度的一般表达式g=______.
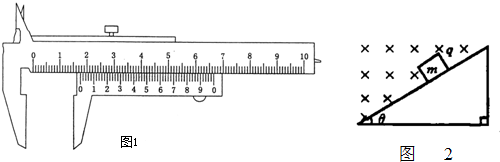
②从图1可知,摆球直径d的读数(分尺标度为5与主尺某一刻度线对齐)为______cm.
(2)将倾角为θ的光滑绝缘斜面放置在一个足够大的匀强磁场中,磁场方向垂直纸面向里,磁感应强度为B,一个质量为m、带电量为q的小物体在斜面上由静止开始下滑(设斜面足够长)如图2所示,滑到某一位置开始离开,求:
①物体带电荷性质______
②物体离开斜面时的速度及物体在斜面上滑行的长度是______
(1)①单摆摆长l=L+
,单摆周期T=d 2
,由单摆周期公式T=2πt n
可知,l g
g=
=4π2l T2
=4π2(L+
)d 2 (
)2t n
;4π2n2(L+
)d 2 t2
②由图1所示游标卡尺可知,游标卡尺主尺示数是1.7cm,游标尺示数是25×0.02mm=0.50mm=0.050cm,
则游标卡尺的示数,即摆球直径为1.7cm+0.050cm=1.750cm;
(2)①带电小物体下滑滑到某一位置开始离开斜面,说明物体受到的洛伦兹力垂直于斜面向上,由左手定则知,小球带负电.
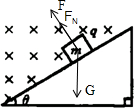
②小物体沿斜面下滑时,受力如图所示;
由牛顿第二定律得:mgsinθ=ma,加速度a=gsinθ,
洛伦兹力F=qvB,当FN=0,即qvB=mgcosθ,
v=
时,小物体开始离开斜面;mgcosθ qB
由匀变速直线运动的速度位移公式可得:
v2-0=2aL,则小物体在斜面上滑行的常识L=m2g(cosθ)2 2q2B2sinθ
故答案为:(1)①
;②1.750cm(2)①负电;②4π2n2(L+
)d 2 t2
.m2g(cosθ)2 2q2B2sinθ
