问题
解答题
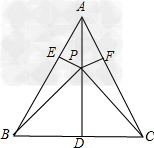
已知，在△ABC中，AB=AC，D是BC边的中点，P是AD上任意一点，PE⊥AB于E，PF⊥AC于F．试说明：
（1）PE=PF；
（2）PB=PC。
答案
证明：（1）∵AB=AC，D是BC边的中点，
∴AD平分∠BAC，
又∵PE⊥AB于E，PF⊥AC于F，
∴PE=PF；
（2）∵AB=AC，D是BC边的中点，
∴AD垂直BC，即AD垂直平分BC，
又∵P是AD上任意一点，
∴PB=PC。
搜题请搜索小程序“爱下问搜题”