问题
选择题
连接对角线垂直的四边形各边中点所得到的四边形是 （ ）
A．正方形
B．菱形
C．矩形
D．等腰梯形．
答案
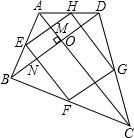
已知：AC⊥BD，E、F、G、H分别为各边的中点，连接点E、F、G、H．
求证：四边形EFGH是矩形
证明：∵E、F、G、H分别为各边的中点，
∴EF∥AC，GH∥AC，EH∥BD，FG∥BD，（三角形的中位线平行于第三边）
∴四边形EFGH是平行四边形，（两组对边分别平行的四边形是平行四边形）
∵AC⊥BD，EF∥AC，EH∥BD，
∴∠EMO=∠ENO=90°，
∴四边形EMON是矩形（有三个角是直角的四边形是矩形），
∴∠MEN=90°，
∴四边形EFGH是矩形（有一个角是直角的平行四边形是矩形）．
故选：C．
