材料题
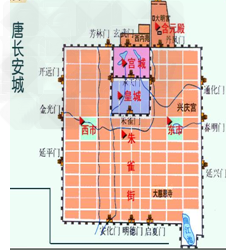
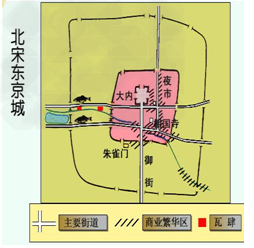
| 阅读下列材料: 材料一:战国商鞅变法规定“戮力本业,耕织致粟帛多者复其身;事末利及怠而贫者,举以为收孥”。 民舍本而事末则好智,好智则多诈,多诈则巧法令。 | ——《史记·商君列传》 | 朕(雍正帝)观四民(指士、农、工、商)之业,士之外,农为最贵。凡士工商贾,皆赖食于农,以故农为天下之本务,而工贾皆其末也。今若于器用服玩,争尚华巧必将多工匠。市肆之中多一工作之人,即田亩之中少一耕稼之人 。 | ——《大清会典事例》 | 材料二:唐都长安平面图 | | 材料三:北宋东京(汴京)城平面图 | | 材料四:明清时期,江南地区出现了一些城市,如棉纺织业发达的松江、陶瓷业发达的景德镇、冶铁业发达的佛山、长江的商品转运码头汉口等地。 请回答: (1)材料一中的“本”与“末”各指什么?这种表达方式能说明作者怎样的观念? | _______________________________________________________________________________ | (2)观察材料二、三两图,与唐代长安比较,北宋东京城市商业有什么新变化?并分析出现这种变化的根本原因。 | _______________________________________________________________________________ | (3)据材料四分析,明清时期城市发展出现的新特点是什么? | _______________________________________________________________________________ | (4)根据材料并结合所学知识,指出中国古代商业发展的主要特点。 | ______________________________________________________________________________________________________________________________________________________________
|