问题
解答题
求经过点A(5,2),B(3,2),圆心在直线2x-y-3=0上的圆的方程。
答案
解:设圆心P(x,y),则由|PA|=|PB|得:(x0-5)2+(y0-2)2=(x0-3)2+(y0-2)2,
又2x0-y0-3=0,两方程联立得: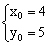 ,|PA|=
,|PA|=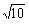 ,
,
∴圆的标准方程为(x-4)2+(y-5)2=10。
求经过点A(5,2),B(3,2),圆心在直线2x-y-3=0上的圆的方程。
解:设圆心P(x,y),则由|PA|=|PB|得:(x0-5)2+(y0-2)2=(x0-3)2+(y0-2)2,
又2x0-y0-3=0,两方程联立得: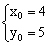 ,|PA|=
,|PA|=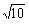 ,
,
∴圆的标准方程为(x-4)2+(y-5)2=10。